Vetores em duas dimensões

Atualizado em 03/03/2024

O que são vetores?

Uma reta orientada é uma reta que possui um sentido de percurso considerado positivo e indicado por uma seta. Um segmento orientado é determinado por um par ordenado de dois pontos no espaço onde o primeiro é a origem e o segundo a extremidade do segmento. Por exemplo um segmento que vai do ponto \(A\) até o ponto \(B\) é denominado de \(\overline{AB}\). E desenhado conforme a Figura 1.

Figura 1 - segmento de reta orientado AB

Um segmento de reta \(\overline{CD}\) possui a mesma direção de \(\overline{AB}\) se a reta suporte que contém os segmentos são paralelas ou coincidem.

Somente quando dois segmentos de reta possuem a mesma direção é que se pode comparar os sentidos dos segmentos.

Dois segmentos de reta são equipotentes quando possuem a mesma direção, sentido e comprimento. E é representado geometricamente por \(\overline{AB}\sim \overline{CD}\).

Figura 2 - segmentos de reta equipotentes

Um vetor é o conjunto de todos os segmentos de reta equipotentes.

Quando observamos a natureza podemos quantificar suas grandezas com números, como por exemplo, a massa dos corpos, a temperatura, o comprimento, o tempo. Não há necessidade de outra informação além do dado numérico para se entender o seu significado. Esse tipo de grandeza é chamada de escalar. No entanto, algumas grandezas físicas, como a velocidade e força, necessitam da representação da direção e sentido para que se compreenda seus efeitos e interações com outras grandezas.

Espaço Vetorial

Seja \(V\) um conjunto não vazio munido das operações de adição “\(+\)” e multiplicação por escalar “\(\cdot\)” fechadas em \(V\). Ou seja:

\(\forall \; \mu,\, \nu \in V,\; \mu+\nu \in V \label{1}\tag{1}\\\) \(\forall \; \alpha\in\mathbb{R},\forall \; \mu\in V,\; \alpha\mu \in V \label{2}\tag{2}\)

Ao que se segue os seguintes postulados em relação a adição e multiplicação:

Axiomas da adição

Associatividade

\[\begin{equation} (\mu+\nu) + \omega = \mu + (\nu+\omega)\quad \forall\; \mu,\nu,\omega \in V \end{equation}\tag{3}\]

Comutatividade

\[\begin{equation} \mu+\nu = \nu + \mu \quad \forall\; \mu,\nu \in V \end{equation} \tag{4}\]

Elemento neutro (Identidade)

\[\begin{equation} \exists\,0 \in V,\; \forall\; \mu \in V\, \text{tal que}\; \mu+0=0+\mu=\mu \end{equation}\tag{5}\]

Elemento oposto

\[\begin{equation} \forall\; \mu \in V,\; \exists (-\mu) \in V\; \text{tal que}\; \mu+(-\mu) = (-\mu)+\mu = 0 \end{equation}\tag{6}\]

Axiomas da multiplicação

para:

\[\forall \; \mu,\nu \in V \;\text{e}\; \forall\; \alpha, \beta \in \mathbb{R}\]

temos que:

Associatividade

\[\begin{equation}(\alpha\beta)\mu = \alpha(\beta\mu) \end{equation}\tag{7}\]

Distributividade em relação a adição

\[\begin{equation} \begin{split} (\alpha+\beta)\mu &= \alpha\mu+\beta\mu \\ \alpha(\mu+\nu) &= \alpha\mu+\alpha\nu \end{split} \end{equation}\tag{8}\]

Elemento neutro (Identidade)

\(\begin{equation} 1\mu = \mu \end{equation}\tag{9}\)

Assim denotamos o espaço vetorial \((V, +, \cdot)\) ou simplesmente \(V\) quando estiver claro suas operações.

Generalizações dos espaços vetoriais

Da definição acima podemos obter espaços vetoriais diversos como \(\mathbb{R}^2\) ou \(\mathbb{R}^3\) ou do conjunto das matrizes com \(m\) linhas e \(n\) colunas, \(M_{(m,n)}\). Assim dependendo do espaço vetorial considerado seus vetores serão elementos do conjunto correspondente e obedecerão os axiomas relativos a adição e multiplicação já descritos.

O espaço vetorial \(\mathbb{R}^2\)

Por exemplo o conjunto \(V \in \mathbb{R}^2=\{(x,y)\mid x,y\in \mathbb{R}\}\) é um espaço vetorial com as operações \(\eqref{1}\) e \(\eqref{2}\) descritas da seguinte forma:

Adição de vetores em \(\mathbb{R}^2\)

\((x_1,y_1)+(x_2,y_2) = (x_1+x_2,\, y_1+y_2) \label{add:vetor}\tag{10}\)

Multiplicação por escalar

\(\alpha(x,y) = (\alpha x,\, \alpha y) \label{mul:escalar}\tag{11}\)

O espaço vetorial \(V\) é definido como um par ordenado de números reais. A magnitude dos vetores em \(\mathbb{R}^2\) pode ser calculada medindo-se a distância entre o ponto de origem e a extremidade do vetor da seguinte maneira:

\[\text{se}\; \vec{v} = (v_x,v_y) \in \mathbb{R}^2,\; \text{então},\; \|\vec{v}\| = \sqrt{v_x^2 + v_y^2}\] \[\begin{align*} \text{se}\; \vec{v} &= (15,8) \; \text{temos:} \\ \|\vec{v}\| &=\sqrt{15^2+8^2} \\ \|\vec{v}\| &= 17\\ \end{align*}\]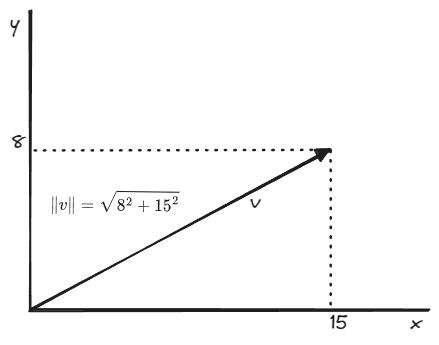

módulo de um vetor em duas dimensões

Figura 3 - Magnitude do vetor <15,8>

Vamos criar uma classe em python que represente nossa definição matemática do espaço vetorial euclidiano em duas dimensões.

import numpy as np # Importa a biblioteca numérica

# Cria a classe Vetor que é um vetor de duas dimensões
class Vetor(object):

  # define os componentes do vetor como (x,y) ao inicializar uma instância
  def __init__(self, x, y):
    try:
      self.x = float(x)
      self.y = float(y)
    except ValueError:
      raise ValueError('x and y devem ser números reais')

  # implementa a multiplicação do vetor por um escalar Vetor * n
  def __mul__ (self, scalar):
    ''' Multiplica um vetor por um escalar elemento por elemento'''
    # tenta converter c para um número do tipo float e gera um erro caso não for possível
    try:
      scalar = float(scalar)
    except ValueError:
      raise ValueError(f'O argumento={scalar} deve ser um número real')
    # retorna um vetor com o produto da operação
    return Vetor(scalar*self.x, scalar*self.y)

  # método caso a multiplicação ocorra à direita n * Vetor
  def __rmul__(self, scalar):
        return self * scalar

  # calcula o produto interno entre dois vetores
  def dot(self, other):
    ''' Calcula o produto interno de um vetor pelo outro. '''
    if type(other) != Vetor:
      raise ValueError(f'O argumento={other} deve ser um Vetor')
    return self.x * other.x + self.y * other.y

  # calcula o produto vetorial ou cruzado
  def cross(self, other):
    ''' Calcula o produto vetorial (cross product) de um vetor pelo outro. '''
    if type(other) != Vetor:
      raise ValueError(f'O argumento={other} deve ser um Vetor')
    return self.x * other.y - self.y * other.x

  # adiciona dois vetores
  def __add__ (self, other):
    ''' Adiciona vetor v e w de mesma dimensão (cardinalidade)'''
    return Vetor(self.x+other.x, self.y+other.y)

  # subtrai dois vetores, adicionando o primeiro com o oposto do segundo
  def __sub__(self, other):
    ''' Calcula a subtração de um Vetor pelo outro como a soma do primeiro com o inverso do segundo elemento da tupla '''
    other = -1 * other
    return self + other

  @property
  def magnitude(self):
    ''' Calcula a magnitude do vetor em R^2 como a distância entre o ponto de origem e da extremidade do Vetor '''
    return np.sqrt(self.x**2 + self.y**2)

  def __eq__ (self, other):
    if type(other) != Vetor:
      raise ValueError(f'O argumento={other} deve ser um Vetor')
    return self.x == other.x and self.y == other.y

  def __neq__(self, other):
    return not self.__eq__(other)

  def __repr__(self):
    return f'Vetor({self.x}, {self.y})'

Abaixo vamos criar alguns vetores e escalares e após isso vamos testar os axiomas aditivos e multiplicativos que descrevemos acima:

import unittest

# Vamos recriar as variáveis para o teste
a = 2.0
b = 3.0

u = Vetor(2,2)
u2 = Vetor(2,2)
v = Vetor(3,0)
w = Vetor(5,6)
nulo = Vetor(0,0)

class TestMetodosClasse(unittest.TestCase):
  def testa_igualdade(self):
    self.assertEqual(u,u2)

  def testa_desigualdade(self):
    self.assertNotEqual(u,w)

  def testa_multiplicação(self):
    self.assertEqual(u*2,2*u)

  def testa_magnitude(self):
    self.assertEqual(u.magnitude, np.sqrt(u.x**2+u.y**2))

  def testa_dot(self):
    self.assertAlmostEqual(u.dot(v)/(u.magnitude*v.magnitude), np.cos(np.pi/4))

class TestAxiomasAdição(unittest.TestCase):
  def testa_associatividade(self):
      self.assertEqual((u+v)+w, (v+w)+u)

  def testa_comutatividade(self):
      self.assertEqual(u+v, v+u)

  def testa_identidade(self):
      self.assertEqual(u+nulo, u)

  def testa_oposto(self):
      self.assertEqual(u+(u*-1), nulo)

class TestAxiomasMultiplicação(unittest.TestCase):
  def testa_associatividade(self):
      self.assertEqual((a*b)*u, a*(b*u))

  def testa_distributividade_vetorial(self):
      self.assertEqual((a+b)*u, (a*u)+(b*u))

  def testa_distributividade_escalar(self):
      self.assertEqual(a*(u+v), a*u+a*v)

  def testa_identidade(self):
      self.assertEqual(1*u, u)

unittest.main(argv=[''], exit=False)

Representando graficamente os vetores em \(\mathbb{R}^2\)

Vamos representar graficamente nosso vetor de duas dimensões e posicioná-lo na origem do plano cartesiano. Para isso criaremos um vetor \(\vec{u}\) que representa duas unidades no eixo x e três unidades no eixo y. \(\vec{u}=(2,3)\)

Lembrando que \(\vec{u}\) é um representante dos vetores \((2,3)\). Escolhemos de forma arbritária o vetor nulo \(\vec{O}\) como origem para plotagem de \(\vec{u}\). Perceba como o vetor representa um ‘deslocamento’ de duas unidades no eixo \(x\) e 3 unidades no eixo \(y\). Para esses vetores unitários \((0,1)\) e \((1,0)\) dá-se o nome de versor. Encontra-se o vetor unitário normalizado de \(\vec{u}\) como produto da razão de \(\vec{u}\) pela sua magnitude:

\[\vec{r}=\frac{\vec{u}}{\|u\|}\]

As componentes unitárias do resultado da operação possuem mesmo sentido e direção que o vetor \(\vec{u}\) mas magnitude um. As componentes no plano coordenado cartesiano são grafados como \(\hat{i}\) e \(\hat{j}\) no eixo \(x\) e \(y\) respectivamente. Algebricamente o vetor \(\vec{u}\) pode ser representado como a soma dos versores.

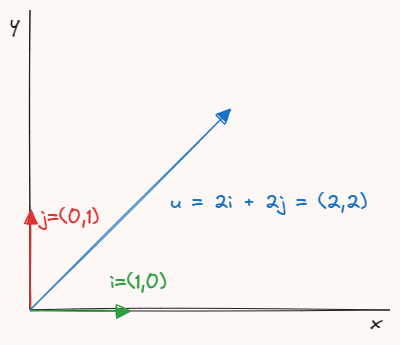
representação versor

Figura 4 - Representação dos vetores unitários

# importa a biblioteca de visualização do python
import matplotlib.pyplot as plt

# cria nosso vetor
u = Vetor(2,3)

# cria o vetor nulo
O = Vetor(0,0)

# cria a figura onde serão grafados os vetores
fig, ax = plt.subplots()

# define o tamanho da nossa tela de plotagem
ax.set_xlim(-1,3)
ax.set_ylim(-1,4)

# cria a figura do nosso vetor com origem em O
ax.quiver(O.x, O.y, u.x, u.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='g')

# mostra o gráfico na tela
plt.show()

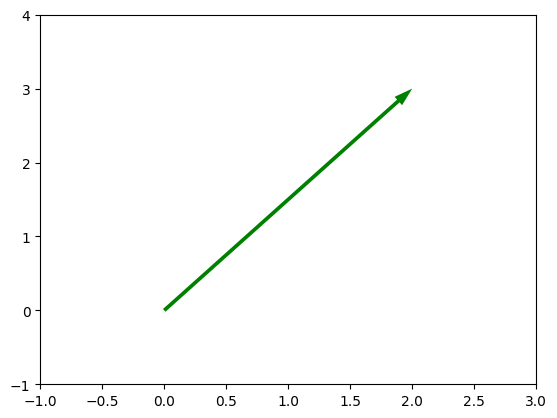
representação de um vetor no plano coordenado

Figura 5 - Vetor u=(2,3)

Se multiplicarmos \(\vec{u}\) por 2 ou dobraremos a sua magnitude (comprimento) mantendo sua direção e sentido. Multiplicar por -1 inverte o sentido do vetor. (Figura 6)

fig, ax = plt.subplots()
ax.set_xlim(-1,5)
ax.set_ylim(-5,10)

# aumenta o nosso vetor u em 2 vezes
v = 2 * u

# inverte o vetor u
w = -1 * u

# cria a figura do u com origem em O
ax.quiver(O.x, O.y, u.x, u.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='g')
# cria a figura do segundo u com origem em no primeiro u
ax.quiver(u.x, u.y, u.x, u.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='g')
# cria a figura do vetor v
ax.quiver(O.x, O.y+1, v.x, v.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='r')
# cria o vetor w
ax.quiver(u.x, u.y-1, w.x, w.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='y')
plt.show()

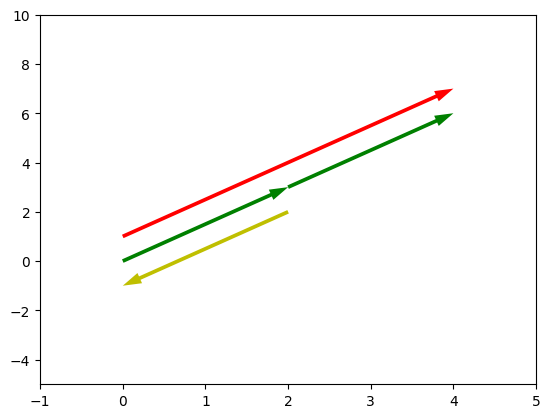
produto escalar de um vetor

Figura 6 - u em verde, v em vermelho e -u em amarelo

Iremos agora somar dois vetores e observar sua representação no espaço cartesiano.

v = Vetor(0,4)
# soma v com o vetor u
r = v+u

fig, ax = plt.subplots()
ax.set_xlim(-2,5)
ax.set_ylim(-2,10)

# vetor u
ax.quiver(O.x, O.y, u.x, u.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='g')

# vetor v
ax.quiver(O.x, O.y, v.x, v.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='b')

# vetor resultado
ax.quiver(O.x, O.y, r.x, r.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='r')

plt.show()

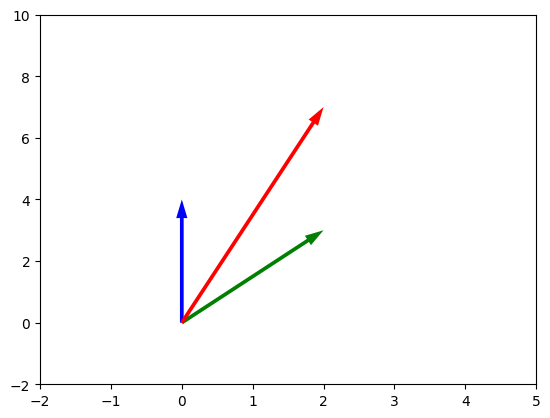
adição de vetores

Figura 7 - Representação da adição de dois vetores. Vetor r em vermelho é o resultado da adição de u+v

Podemos representar \(\vec{u}\) com sua origem na extremidade de \(\vec{v}\). Agora é possível ver \(\vec{r}\) como resultado de \(\vec{r}=\vec{u}+\vec{v}\). Assim \(\vec{r}\) se inicia na origem de \(\vec{u}\) e termina na extremidade de \(\vec{v}\).

fig, ax = plt.subplots()
ax.set_xlim(-1,5)
ax.set_ylim(-1,10)

# vetor u
ax.quiver(v.x, v.y, u.x, u.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='g')

# vetor v
ax.quiver(O.x, O.y, v.x, v.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='b')

# vetor resultado
ax.quiver(O.x, O.y, r.x, r.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='r')

plt.show()

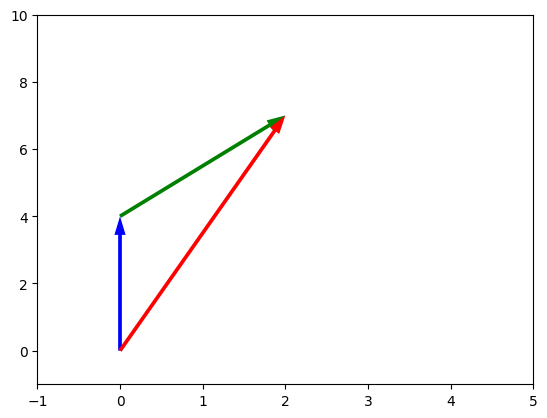
regra do paralelogramo

Figura 8 - Representação da adição de dois vetores. Vetor r em vermelho é o resultado da adição de u(azul)+v(vermelho)

É possível representar a diferença entre dois vetores como a soma de um vetor com o oposto do segundo.

\[\vec{v}-\vec{u} = \vec{v}+(-\vec{u})\]

fig, ax = plt.subplots()
ax.set_xlim(-5,5)
ax.set_ylim(-5,10)

w = u-v

# vetor u
ax.quiver(O.x, O.y, u.x, u.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='g')

# vetor v
ax.quiver(O.x, O.y, v.x, v.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='b')
ax.quiver(O.x, O.y, -v.x, -v.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='black')

# vetor resultado
ax.quiver(O.x, O.y, w.x, w.y, angles='xy', scale_units='xy', headaxislength=5, scale=1, color='r')

plt.show()

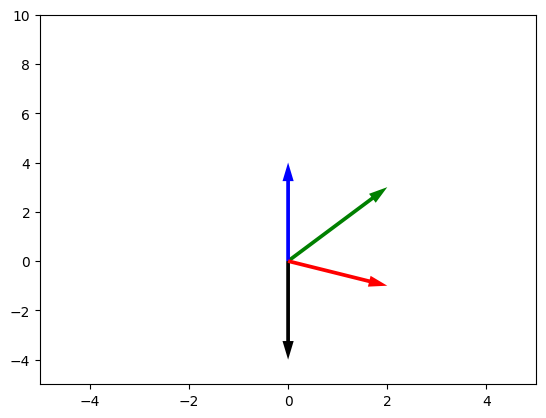
subtração de vetores

Figura 9 - Representação da subtração de dois vetores. Vetor r em vermelho é o resultado da subtração de u(verde)-v(azul) em preto (-v)

No notebook com o código do texto é possível modificar os valores e brincar um pouco com as representações geometricas dos vetores no plano. Clique aqui!